建议阅读Is the deconvolution layer the same as a convolutional layer?

　　要知道两者的区别，我觉得最直观的方式就是从他们的实现方式上去分析。首先来看下反卷积是如何实现的，首先看下面反卷积的运算流程图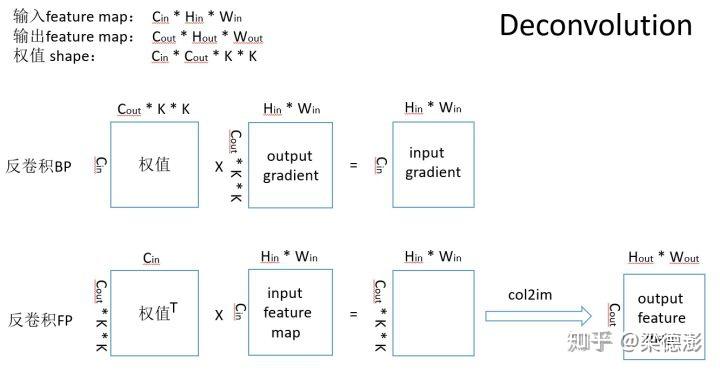：https://zhuanlan.zhihu.com/p/65248401

　　反向过程我们不需要关注只看前向过程，看流程图最下面的一行。反卷积的前向过程就是首先做了一个矩阵乘法（或者也可以用1x1的卷积来实现），把输入 feature map 的通道数从 Cin 变成 Cout * K * K，这时候 feature map 的大小还是保持 Hin * Win 的，那反卷积是如何实现把 feature map变大的呢，其实就是接下来的一步col2im操作，这个相当于是卷积里面的 im2col 的逆过程，把中间结果的每一列从一个 Cout * K * K的向量，reshape 成 (Cout, K, K) 的 tensor，然后根据 Cout 的索引把对应 (k, k) 的 patch 回填累加到输出 feature map 对应 channel 的位置上，至于应该把这个patch回填到某张 feature map 的哪个位置上，这个可以说主要是由步长这个参数决定的，就像带步长的卷积，在做卷积操作的时候，窗口会根据步长来滑动，反卷积回填的时候，也是根据步长来滑动回填窗口。但是具体实现的时候没那么简单了，还有其他参数，具体可以参考mxnet里面反卷积的实现。

　　分析完反卷积的运算过程，再来看下上采样+卷积的运算过程，上采样比如双线性插值，就是把feature map根据上采样率插值出更大的feature map，feature map之间的上采样是各自独立的，所以channel数不会改变，然后再跟一个卷积提特征，这一步才可以改变channel数。

　　那既然他们共同的作用都是可以增大 feature map 同时改变 channel 数，那么在实际任务中该如何选择呢。反卷积有个比较大的问题就是，如果参数配置不当，很容易出现输出feature map带有明显棋盘状的现象，为什么呢，就是在col2im，然后回填这一步。

　　下面这个博客就分析的非常好，值得细读：Deconvolution and Checkerboard Artifacts

　　里面提供了可动态配置反卷积的kernel size和stride然后可视化输出结果，可以看到当stride为2的时候，kernel是奇数就会出现网格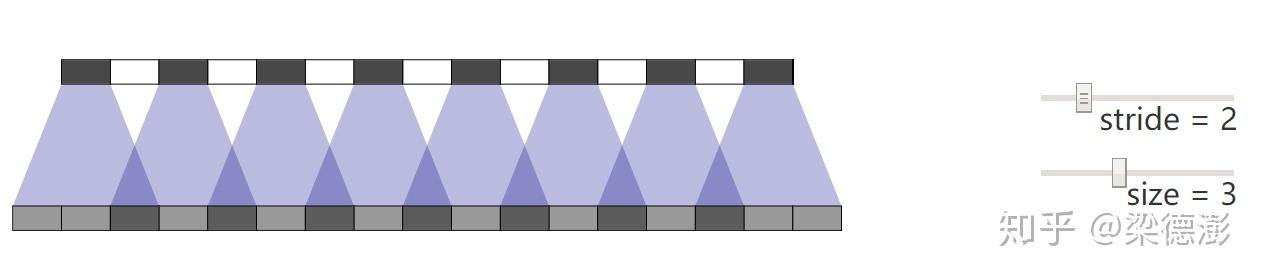：https://distill.pub/2016/deconv-checkerboard/https://distill.pub/2016/deconv-checkerboard/

　　而偶数kernel就不会：https://distill.pub/2016/deconv-checkerboard/https://distill.pub/2016/deconv-checkerboard/

　　而如果是多层堆叠反卷积的话而参数配置又不当，那么棋盘状的现象就会层层传递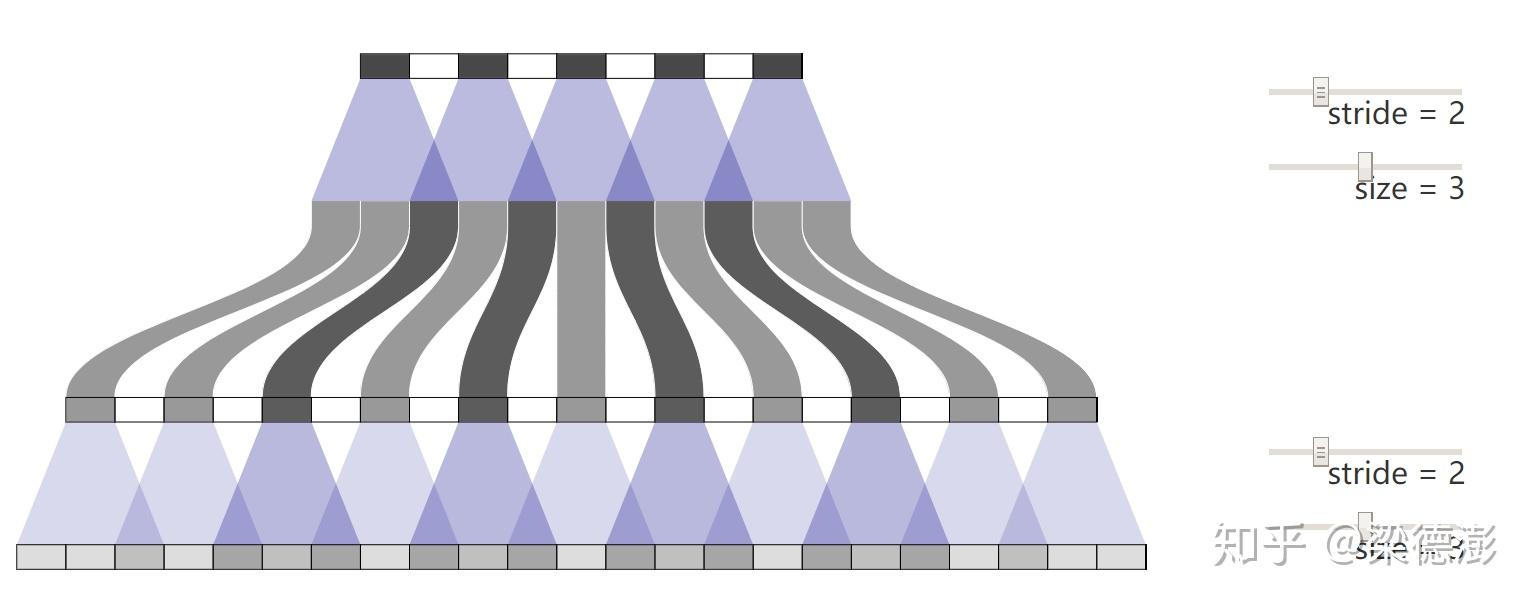：https://distill.pub/2016/deconv-checkerboard/

　　所以当使用反卷积的时候参数配置需要特别的小心。

　　Talk is cheap, show me the code！：）

　　下面就用简单的几句代码来复现使用反卷积可能会带来的的网格问题：

　　这里为了简化，反卷积和卷积的权重都是设为1，而输入与输出 feature map 通道数都是1，输入 feature map 的值都是1，然后来看下反卷积和上采样+卷积的前向结果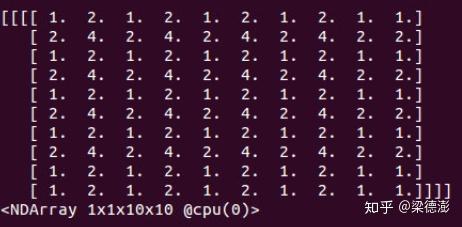：deconvolution, kernel3, stride2bilinear upsample + convolution

　　可以看到，kernel为3，步长为2的情况下，反卷积在不训练的情况下，输出就带有明显很规律的棋盘状。然后我们把kernel改为4，看看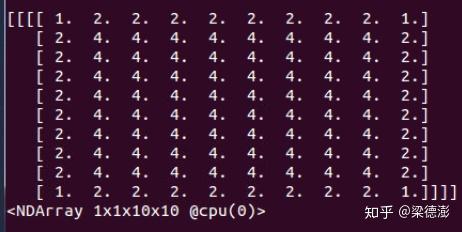：deconvolution, kernel4, stride2

　　所以可以看到，棋盘状消失了。所以在实际应用中对于一些像素级别的预测任务，比如分割，风格化，gan这类的任务，对于视觉效果有要求的，在使用反卷积的时候需要注意参数的配置，或者直接换成上采样+卷积。大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!

　　相关资料：梁德澎：怎样通俗易懂地解释反卷积？

　　梁德澎：估算卷积层与反卷积层运算量

　　总的来说不大信任反卷积，难免有棋盘格效应，跑GAN时很明显。

　　没有什么是上采样+卷积不能解决的，除非网络占用空间实在太大，考虑用反卷积减少一点占用

　　我个人在用的时候没发现两者可能造成的性能上的巨大差别，而且我觉得后者反而更友好，更好理解且容易工程实现。

　　注，反卷积因为没有亚像素插值，还容易造成棋盘格现象

　　上采样+卷积在monodepth里就用了很多

　　不论是语义分割、目标检测还是三维重建等模型，都需要将提取到的高层特征进行放大，此时就需要对feature map进行上采样（也有一些文章称之为升采样，是一个意思，本文均用上采样。） 上采样一些常见的方法有：近邻插值（nearest interpolation）、双线性插值(bilinear interpolation)，双三次插值（Bicubic interpolation），反卷积(Transposed Convolution)，反池化(Unpooling)。 本文对这些方法进行了总结，如有描述不当，欢迎批评指正。

　　本文同步发布在公众号：happyGirl的异想世界 中，欢迎关注~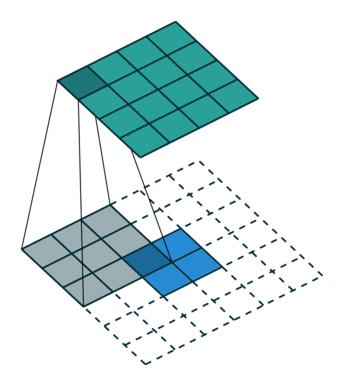

　　最近邻插值法（nearest neighbor interpolation）又称零阶插值,将离待插值最近的已知值赋值给待插值。如图所示，最近邻插值法会直接只算输出像素映射到输入图像坐标系下的点u和近邻四点(n1,n2,n3,n4)之间的距离,取距离u最近的像素点的颜色值(或灰度值)赋给u。计算公式：

　　g(x',y')=f(int(x+0.5),int(y+0.5))

　　其中g(x',y')为输出图像中坐标为(x',y')的像素点的颜色值(或灰度值)，f(x,y)为输入图像中坐标为(x,y)的像素点的颜色值(或灰度值),(x,y)为输出图像上的坐标(x',y')映射到输入图像坐标系下的坐标。int(x)为取整运算。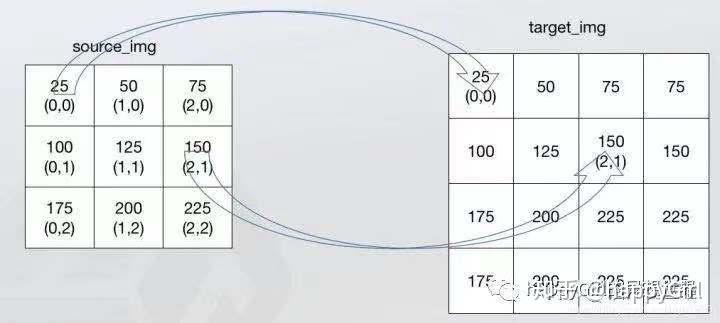

　　上图效果是最近邻法的计算过程示意图，最近邻不需要计算只需要寻找，所以速度最快，但是新图像局部破坏了原图的渐变关系。

　　已知中P1点和P2点，坐标分别为(x1, y1)、(x2, y2)，要计算 [x1, x2] 区间内某一位置 x 在直线上的y值。

　　根据两点求一条直线可知：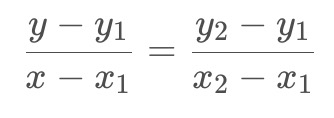

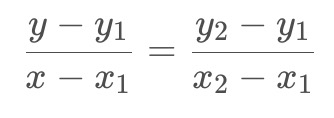
　　整理后得：

　　y1与y2分别代表原图像中的像素值，公式可改写为：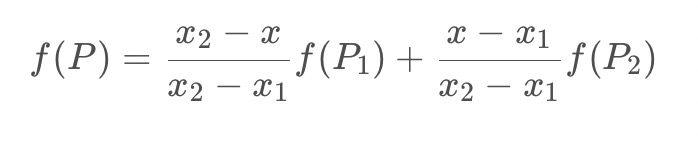

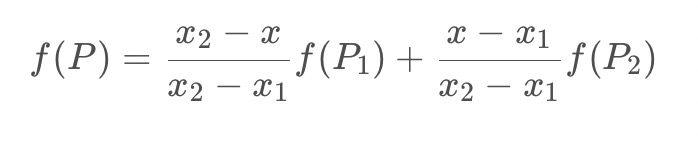
　　双线性插值（bilinear interpolation）又称一阶插值,根据离待插值最近的2*2=4个已知值来计算待插值，每个已知值的权重由距离待插值距离决定，距离越近权重越大。双线性插值是分别在两个方向计算了共3次单线性插值，如图所示，先在x方向求2次单线性插值，获得R1(x, y1)、R2(x, y2)两个临时点，再在y方向计算1次单线性插值得出P(x, y)（实际上调换2次轴的方向先y后x也是一样的结果）。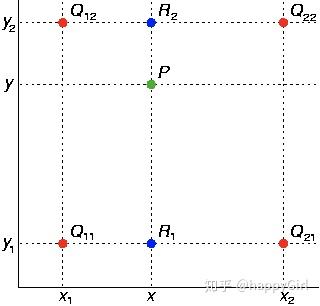

　　双三次插值（bicubic interpolation）也有一些文章会翻译为三线性插值，本文统一同双三次插值。其根据离待插值最近的4*4=16个已知值来计算待插值，每个已知值的权重由距离待插值距离决定，距离越近权重越大。双三次插值通过下式进行计算：

　　或者用一种更加紧凑的形式，

　　

　　计算系数 aij 的过程依赖于插值数据的特性。如果已知插值函数的导数，常用的方法就是使用四个顶点的高度以及每个顶点的三个导数。一阶导数 h'x与 h'y 表示x与y方向的表面斜率，二阶相互导数h''xy表示同时在x与y方向的斜率。这些值可以通过分别连续对x与y向量取微分得到。对于网格单元的每个顶点，将局部坐标（0,0, 1,0, 0,1 和 1,1) 带入这些方程，再解这16个方程。

　　下图来源于wikipedia中词条Bicubic interpolation的插图，感觉还是很生动形象的。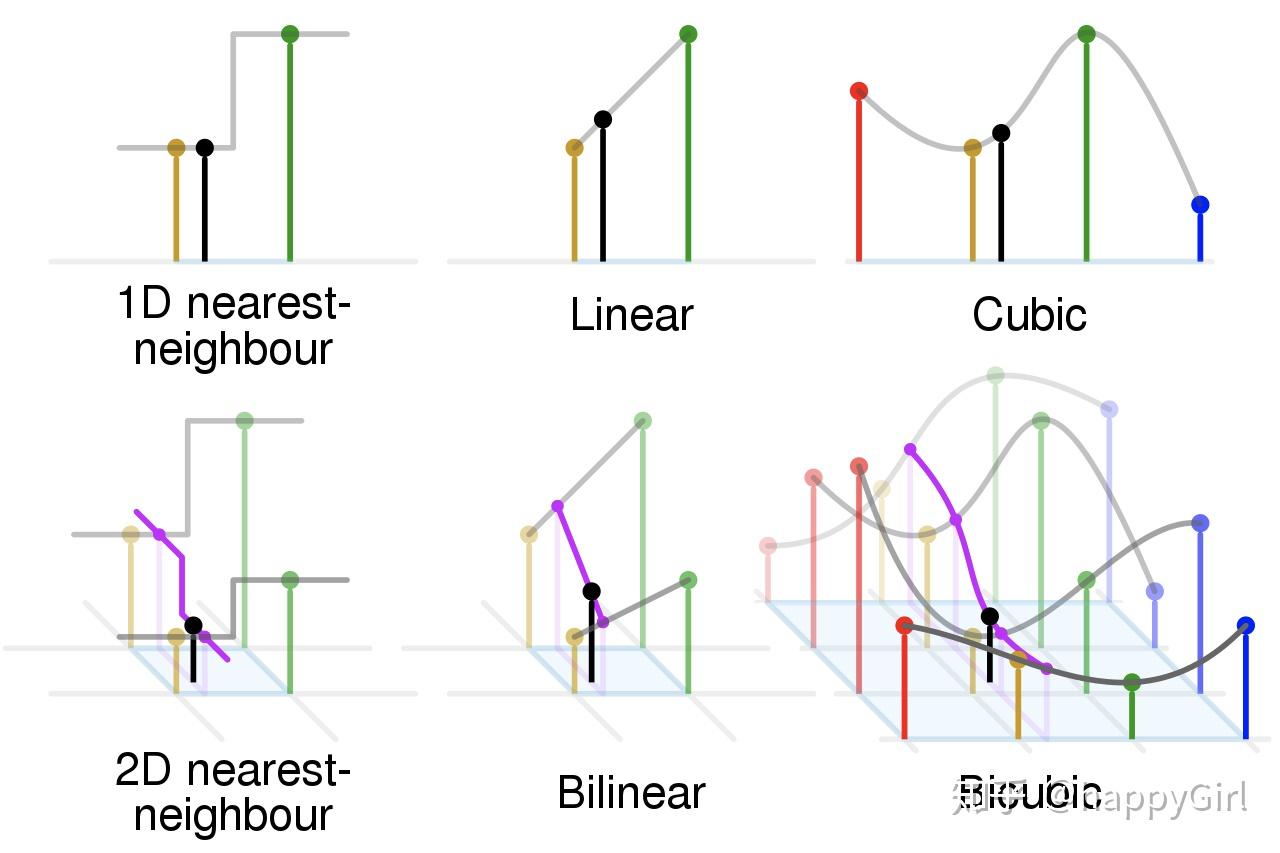

　　反卷积(DeConv)又叫转置卷积(TransposeConv)（更规范的表述），是一种特殊的卷积，常用于实现特征图（Feature Maps）的上采样。采用矩阵乘法的方式考虑卷积的前向和反向过程，分别使用和来相乘，而反卷积的前向和反向过程分别使用和来相乘。

　　关于卷积和反卷积的一些计算原理，小编觉得《A guide to convolution arithmetic for deep learning》写得非常清洗（链接：https://arxiv.org/pdf/1603.07285.pdf）接下来我们将解读反卷积的计算原理，首先我们简单描述一下卷积的计算原理。

　　假设有一个的输入input feature，使用一个的卷积核进行卷积操作，stride=1，padding=0，那么我们可以得到一个的矩阵，如下面所示：

　　接下来我们将以矩阵乘法的方式来描述的卷积运算，Y=CX

　　将input feature 展开成列向量

　　

　　将kernel展开成稀疏矩阵

　　

　　计算 ，并将输出的矩阵reshape成2x2的矩阵，得到与之前相同的结果。

　　反卷积则通过 来恢复到原始的输入的shape，故称之为转置卷积。

　　正如前文所说，反卷积是一种特殊的卷积，总是可以使用一种卷积来模拟反卷积的过程。然而该方式将引入许多‘0’的行和‘0’的列，导致实现上非常的低效。 卷积前向过程会有padding、stride、kernel等参数，我们将通过这些参数来找到与反卷积等价的前向卷积的参数。

　　理解反卷积的计算过程一个核心是连接模式（Connectivity pattern），两个关键是1）zero padding；2）stride < 1。这两种方式均可以实现从低分辨率到高分辨率的映射。

　　首先是zero padding，通过考虑反卷积的连接模式（connectivity pattern）来考虑应该如何padding。请看Figure 4.1中，卷积过程（绿色->蓝色），从4x4的输入得到2x2的输出。现在通过转置卷积过程（蓝色->绿色）将2x2的输入恢复到4x4的输出。那应该padding多少呢大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!？轮到我们的连接模式出场了。考虑卷积过程中，由kernel size，padding，stride决定Green[0, 0]只贡献到了Blue[0, 0]。因此在反卷积过程中，通过padding=2，stride=1来保证连接模式，即Green[0, 0]只从Blue[0, 0]中恢复信息。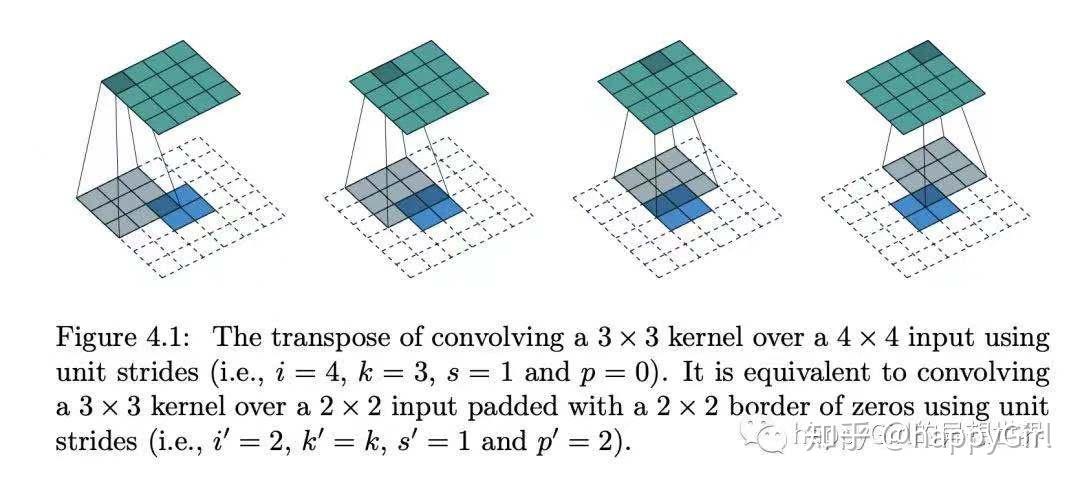

　　然后是stride < 1，当卷积过程中的stride > 1时，即需要stride < 1来保证原来的连接模式以及从低分辨率到高分辨率的映射。如图Figure 4.5中，原来的卷积stride=2，因此在转置卷积过程中需要stride=1/2，由于stride是正整数，因此通过在输入特征图中（蓝色）进行'0'行和'0'列的插入，约束stride=1来等价得到转置卷积需要的stride=1/2。'0'行和'0'列插入的数量一个如何设置呢？假设原始卷积过程的stride=s，现在转置卷积过程中需要stride=1/s。那么我们插入s-1个'0'行或者0'列'，并约束stride=1，那么我们得到的等价的stride=1/s。直观的理解，插入'0'行或者'0'列后，stride=1需要移动原先的s倍才能遇到插入前的那个像素点，因此等价于stride=1/s

　　卷积的情况很多：不同padding、stride、kernel size，其对应反卷积的操作也不尽相同，下面我们分情况列举

　　假定输入图片大小为4x4，卷积核大小为3，步长为1，无padding，即

　　i = 4, k = 3, s = 1, p = 0

　　其对应反卷积则是在：

　　i = 2, k = 3, s = 1

　　的情况下补0达到输出图片维度为4x4的目的。

　　根据connectivity pattern原理以及上文提及的第一个关键点zero padding，在输入图片上padding=2即可，如图Figure 4.1所示

　　可以总结下：

　　对于k = k, s = 1, p = 1的卷积来说，其反卷积等同于s_de = 1, k_de = k , p_de = k - 1的卷积，其输出大小为：

　　o’ = i’ + (k - 1).

　　对于i=5,k=4,p=2的卷积，其反卷积如图Figure 4.2所示

　　同样的，根据connectivity pattern的zero padding 关键，进行zero padding。 总结：

　　对于k = k, s = 1, p = p的卷积来说，其反卷积等同于s_de = 1, k_de = k , p_de = k-p-1的卷积，其输出大小为：

　　o’ = i' + (k - 1) - 2p

　　对于k = 2n+1, s = 1, p = 的卷积来说，其反卷积等同于s_de = 1, k_de = k , p_de = p的卷积，其输出大小为：

　　

　　图Figure4.3是i = 5, k = 3, p = 1的一个例子

　　更多情况可参见公众号推文

　　反卷积会产生棋盘效应一直被人所诟病。当我们仔细的看神经网络生成的图片时，我们常常会看到一些棋盘格样式的瑕疵。这种棋盘格瑕疵在强烈色彩的图片中会尤为凸显。

　　当我们用神经网络生成图片时，我们会从低分辨率和高层次的描述中构建它们。这使得网络可以向粗略的图片中填充细节。我们可以使用反卷积实现从低分辨率到高分辨率，允许模型用小图中的每一个点来绘制更大的一块正方形。

　　不幸的是，反卷积很容易有不均匀的重叠，特别是当核尺寸不能被步长整除的时候，反卷积会有不均匀的重叠。虽然理论上神经网络可以仔细的学习权重参数来避免产生这种瑕疵，但是事实上神经网络不能完全避免这种情况的发生。

　　这种重叠的样式体现在两个维度上。两个坐标轴上不均匀的重叠相乘，得到了类似棋盘格一样不同大小的特性。不均匀的重叠在二维的情况下会更严重。因为当两种模式相乘，不均匀的模式会被平方。比如，在一维的情况下，一个步长为2，尺寸为3的反卷积输出数量为输入的两倍，但是在二维情况下，系数就变为了4。

　　如今，神经网络通常用在生成图像的时候通常用多层反卷积，通过不断的迭代从低像素图片构建高像素图片。尽管这些堆叠的反卷积可以在一定程度上消除棋盘效应，但他们经常复合，在不同尺度上产生这种瑕疵。

　　为了改善棋盘效应，一些模型会在最后一层加上步长为1的反卷积，他们确实在减弱瑕疵方面有一定的效果，可以消除频率整除其大小的棋盘格效应，也可以减少其他频率小于尺寸的瑕疵，但是依然无法完全消除棋盘效应。

　　理论上，我们的模型可以仔细地写入不均匀重叠的位置，使得其均匀写入，达到平衡。这种平衡的操作的实现是很困难的，特别是当多个通道相互影响的时候。避免棋盘格瑕疵会很大程度上限制过滤器，牺牲模型的容量。实际上神经网络很难完全避免这些问题，不仅仅是不均匀重叠的模型不能避免这种问题，均匀重叠的模型也会学习产生同样的瑕疵的卷积核。尽管不是像不均匀重叠的默认行为，对于均匀重叠的反卷积仍然是很容易产生瑕疵的。

　　完全避免棋盘格效应对于过滤器来说仍然是一个很严重的限制，这里可能有很多因素在起作用。比如说，在生成对抗网络中，再好的情况下，反卷积也是脆弱的，就算很小心的调整尺寸的大小，生成器、梯度的原理导致其依然很容易表达瑕疵，反卷积不生成瑕疵几乎是不太可能的。

　　有没有对于棋盘格效应更有抵抗能力的上采样方法呢？

　　方法之一是确保反卷积核的大小可以被步长整除，从而避免重叠问题。这等价于最近成功用于图像超分辨率解析的技术“子像素卷积”（sub-pixel convolution） (Shi, et al., 2016b)。尽管这种方法有效，但反卷积仍然容易产生棋盘效应。

　　另一种方法是将上采样分离为较高分辨率的卷积到计算特征。例如，可以调整图像大小（使用最近邻居插值或双线性插值），然后进行卷积层，类似的方法有用在图像超分辨率（例如，Dong，et al。，2015）上。

　　也可以结合缩放卷积。反卷积与缩放卷积（resize-convolution）方法都是线性操作，可以用矩阵去解释。对于每个输出窗口，反卷积操作的输入唯一，缩放卷积会用集中权重的方式来抑制高频瑕疵。

　　反池化（unpooling），也有一些文章会翻译为上池化，总之都是一个意思。Unpooling通常是卷积过程中max pooling的逆操作。这是论文《Visualizing and Understanding Convolutional Networks》中提出的思想。 （论文链接 https://arxiv.org/abs/1311.2901） 反池化是池化的逆操作，是无法通过池化的结果还原出全部的原始数据。因为池化的过程就只保留了主要信息，舍去部分信息。如果想从池化后的这些主要信息恢复出全部信息，则存在信息缺失，这时只能通过补位来实现最大程度的信息完整。池化有两种：最大池化和平均池化，其反池化也需要与其对应。

　　首先还原成原来的大小，然后将池化结果中的每个值都填入其对应原始数据区域中相应位置即可。 平均池化和反平均池化的过程如下：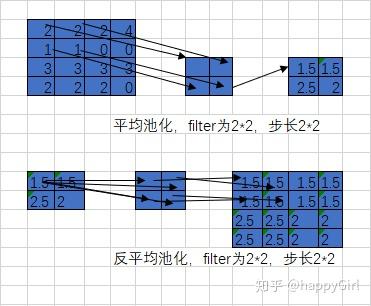

　　要求在池化过程中记录最大激活值的坐标位置，然后在反池化时，只把池化过程中最大激活值所在位置坐标值激活，其他的值设置为0.当然，这个过程只是一种近似。因为在池化过程中，除了最大值的位置，其他的值也是不为0的。最大池化和反最大池化的过程如下：

　　https://distill.pub/2016/deconv-checkerboard/https://zhuanlan.zhihu.com/p/41427866https://zhuanlan.zhihu.com/p/110754637https://zh.wikipedia.org/wiki/%E5%8F%8C%E4%B8%89%E6%AC%A1%E6%8F%92%E5%80%BChttps://blog.csdn.net/chengqiuming/article/details/80300284https://arxiv.org/pdf/1603.07285.pdf大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!